Making Seamless Hex Tiles

I know I haven't posted on this blog in ages, but recently I came across a world-building problem for which I could not find a suitable answer on the Internet: How to make seamless hex map tiles.

Where it seems like a very difficult task (matching up 3 pairs of borders) it actually has a very simple and elegant solution.

First, most major image manipulation programs have a "make seamless" feature that tiles and blurs over an image to make it seamless on four sides.

For example: The GIMP's function can take any rectangular image and make it tileable by using the "Make Seamless" command. Unfortunately, it doesn't directly work with other shapes (like our hex) or some arbitrary outline.

However, this filter will work perfectly to give us exactly what we want, as we can "simplify" a hex map into a rectangular map which it *can* make seamless for us.

Imagine a map of tiled hexes and take a close look at the pattern:



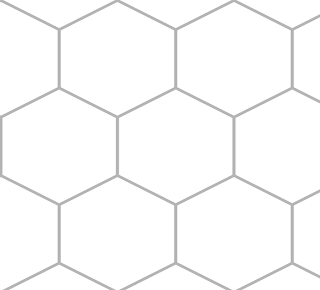
It's regular. It repeats.

Since the GIMP can tile rectangles, can we express this sort of repetition as a set of rectangles?

You bet we can:


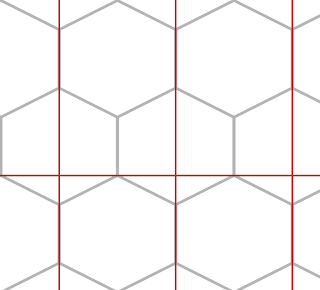
So now we're dealing with the following rectangular unit to tile:


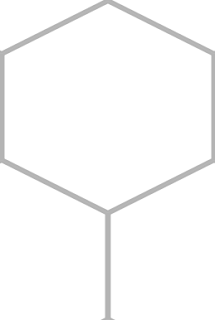
Assuming your hex occupies a square image, the rectangle is 1 unit long by 1.5 units tall.

So all we need to do is go into the GIMP and make a rectangle that fits those dimensions and make it seamless. In my case, since my hex tiles were 256x256 pixels, this made the rectangle 256x384 pixels:

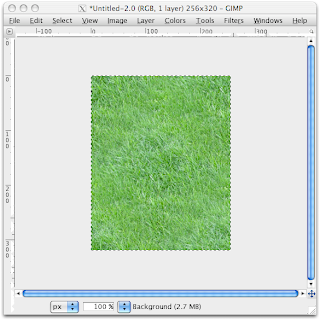(Here's the seamless texture. A small plot of grass hit with the Filters->Map->Make Seamless command.)

Next, you'll need to plop the texture down onto a hex outline so that it is flush with both vertical sides. Even though the texture is a full half taller than your hex, it doesn't matter. Provided that the edges are flush and the entire hex is full of the texture, all you need to do is clip it to the hex's outline.

I've done this in Inkscape, where I've made my hex outline using the Polygon tool, and then used the Clip->Set command to trim the duplicated textures to the hex.


Voilà! You now have a seamless, tileable hex!

Peace,
-Steve

Simulating the Large-Scale Structure of the Cosmos

In my previous article, we discussed Perlin Noise and how it can generate textures that seem very natural. In this article, we're going to see how we can use Perlin Noise to generate a convincing image of the large-scale structure of the cosmos.

What is this large scale structure? Wikipedia states:

"In physical cosmology, the term large-scale structure refers to the characterization of observable distributions of matter and light on the largest scales (typically on the order of billions of light-years). Sky surveys and mappings of the various wavelength bands of electromagnetic radiation (in particular 21-cm emission) have yielded much information on the content and character of the universe's structure. The organization of structure appears to follow as a hierarchical model with organization up to the scale of superclusters and filaments. Larger than this, there seems to be no continued structure, a phenomenon which has been referred to as the End of Greatness." - http://en.wikipedia.org/wiki/Large-scale_structure_of_the_cosmos - Jan 5th 2007

These "superclusters" and "filaments" together create a structure that looks like a piece of open-cell foam or nerve cells. For example:

(http://www.mso.anu.edu.au/2dFGRS/)

Now if you can remember back to what we discussed about Perlin Noise, when we output a representation of a 2 dimensional slice of it, it looks like a fractal terrain map.


This above image is taken with a $size factor of 42. It isn't very helpful in creating something that has nodes, filaments and voids inbetween. However, your standard Perlin Noise algorithm, like the one we use in this project, returns a value between 1 and -1. This means that there's a 0 in the middle somewhere that occurs regularly, so if we take the absolute value of the noise we get the following:


Which, if you look at the picture of the redshift survey, this looks closer to a negative image. If we flip the noise (1-|noise|) we get the following:


Much closer to what we're after, but still not quite it. Fiddling around with adding in some contrast, we can eventually arrive at a very nice model:


The above image is based off of the quantity of one minus the absolute value of noise to the 8th power (1-|noise|)⁸. If we zoom out a bit (bringing the $size down to 16) we can see how it mimics the distribution of clusters, filaments, and voids rather well:


Using this noise technique as our base, we can make a very nice looking large-scale structure. Keeping the $size to around 40-ish (I'm rather partial to 42) leaves each [x,y,z] coordinate to the scale of approximately 1 megaparsec.

In the next article, I'll show how we can use this distribution to mimic the appropriate number of galaxies in each megaparsec along with their distribution and a way to display them on the fly through a simple point-and-click web interface. Furthermore, I'll show you how to do it in such a way that it won't cause the PHP script to slow to a grinding halt.

Peace,
-Steve

Perlin Noise - Your New Best Friend

Perlin Noise is a technique to create natural looking textures and movements by using pseudorandom numbers that was designed by a rather clever computer scientist, Ken Perlin, who is a Professor at New York University.

Instead of trying to explain what it is and how it works (aka "reinvent the wheel"), I'll instead point you in the direction of Professor Perlin's own words. Read this; absorb this:

http://www.noisemachine.com/talk1/

So now that you're familiar with the basics and how things work, here are two more articles about how Perlin Noise can be used and the basic math behind it:

http://student.kuleuven.be/~m0216922/CG/perlinnoise.html
http://freespace.virgin.net/hugo.elias/models/m_perlin.htm

(If these articles are ever taken down, I'll write up something even better here when I have the time.)

Perlin Noise is a marvelous tool for modeling natural structures, as the field it generates is inherently procedural (so we can calculate things at any point simply knowing the seed) and fractal (like many natural structures). Once you're able to master Noise, you'll be able to master some very good-looking visualizations.

Now for my purposes, I took the Improved Noise function that Perlin wrote, himself, and ported it to PHP:

http://research.thenerdtank.com/therandomuniverse - Click on Perlin.class.txt

You'll also note that I put together two additional functions which come in handy when you quickly need less than 3 degrees of noise.

Using the code above, I was able to get the following results when creating an image:

Since the Perlin Noise function gives a number between -1 and 1, inclusive, the picture on the right is divided by two plus one (noise/2+1), where the picture on the left is its absolute value (|noise|).

Now, using this noise function, in our next article we're going to investigate how to decently simulate (for the sake of an RPG) the large-scale structure of the cosmos by modeling the layout of galaxy clusters.

Peace,
-Steve

The Scope of This Project

Alright, before I actually get to the two articles I promised I'd start out with, I feel the need to discuss a bit more about the scope of this project.

The vast majority of widgets that I've put together for my tabletop roleplaying endeavors have been designed for access through a web browser. In the past, I've had character sheets online so that players can update them at home, battle maps with virtual figs projected onto a screen or wall where players can log into a local server and move them across the board, and mapping software that allowed for the players to put their own labels on the map and sort them in real time through Firefox.

All of my widgets I've coded using a combination of PHP (4.x or 5.x) and MySQL, running off of an Apache server, and for this particular project, I intend to do the same.

All diehard programmers now will immediately say, "This certainly imposes some significant restrictions on what you can do," to which I must agree. PHP, being an interpreted language is certainly slower than C++, Visual Basic, or Java, which will cause very complex simulations to slow down to a crawl. Secondly, PHP is only good at exporting to webpages where some people may want to use the techniques in 3D.

I choose to use this combination for two main reasons:

1. Anyone and everyone can view a webpage and click links.
2. It forces me to keep my simulations simple and concise, so others who expound upon my work will have something easily portable to whatever platform they wish.

With the code that I'll share here, you can use it with minimal jiggery-pokery to export to a program such as POVRay to render a high-quality model, and it will be simple enough for you to port it to Java and integrate it with Java3D for visualization. I'll also have a version of all examples I show here up and running over on The Nerd Tank for tinkering.

So, now off onto the next topic: Perlin Noise!

Peace,
-Steve Caruso

Procedural Universe

Finally, I've decided to get back to the purpose that this blog was originally constructed for and that is generating a procedural universe.

What is a "procedural universe" you may ask? In short, it is a convincing enough representation of a fictional universe that is mathematically defined. This would allow for a computer program to generate an entire universe on the fly, only calculating the pieces you're currently looking at rather than having to construct everything at once and then sift through the data.

Imagine: You're viewing an image of the large scale structure of the cosmos. You click on a cluster of galaxies and you zoom in. You then click on a single galaxy and zoom in to where you can see individual stars. Click on a star, and if there are planets around it, they'll display on the screen. Click on a planet, and you'll be able to walk across its terrain. From there, you could, say, click on a city on the planet's map and zoom in to where you can see individual buildings, and from there, click on individual inhabitants of each building.... Or do it in reverse... Whew. :-)

Many people may say, "Well, isn't that something similar to what Maxis is doing with their new game Spore?" ... Similar, I admit. My work on procedural universes started many years before Spore was announced, and its scope was more confined to how it would help out with traditional "pen and paper" roleplaying games (you know, the kind that actually have a storyteller rather than a computer who tells you what happens). As such, the level and attention to detail that I've been going for is much higher than one would find in your average video game.

In the next two articles I post here, I'll be going over the most important tool towards procedural universe generation known to man: Perlin Noise. I'll then follow it up with how to decently simulate the large-scale structure of the cosmos.

From there, my path is still a bit fuzzy, but I promise I'll incorporate random galaxy generation (from elliptical to spiral to irregular), star generation, planet generation using dole's accretion algorithm and other methods, fractal terrain generation with a section on how to calculate map projections and color schemes, city generation, building generation, and many more.

Peace,
-Steve Caruso